Comparación de modelos mediante Factores de Bayes
Cuando trabajamos con datos es común tener varios modelos posibles que podrían explicar esos datos. Algunos modelos son simples (con pocos parámetros) y otros complejos (con más parámetros).
Problema al elegir modelos:
| Si usamos un modelo muy simple | Si usamos un modelo muy complejo |
|---|---|
| ❌ No captura toda la información (sesgo) | ❌ Se ajusta demasiado a los datos (sobreajuste, alta varianza) |
Por eso, necesitamos una manera objetiva de decidir qué modelo es mejor.
¿Qué son los Factores de Bayes (Bayes Factors)?
Los Factores de Bayes (BF) son una herramienta para comparar dos modelos (\(M_0\) y \(M_1\)) según qué tan bien explican los datos.
👉 Se basan en la razón (cociente) entre las verosimilitudes marginales de cada modelo:
\[ BF(M_0, M_1) = \frac{P(X | M_0)}{P(X | M_1)} \]
Donde:
- \(P(X | M_0)\) = Verosimilitud marginal del modelo \(M_0\) dado los datos X
- \(P(X | M_1)\) = Verosimilitud marginal del modelo \(M_1\)
Interpretación intuitiva:
| Valor del BF | Interpretación |
|---|---|
| \(BF > 1\) | Los datos favorecen el modelo \(M_0\) sobre \(M_1\) |
| \(BF < 1\) | Los datos favorecen el modelo \(M_1\) sobre \(M_0\) |
¿Qué es la verosimilitud marginal?
La verosimilitud marginal de un modelo \(M_i\) es:
\[P(X∣M_i)=∫P(X∣θi)P(θi)dθi\]
🔑 Es decir:
- La probabilidad de los datos bajo el modelo \(M_i\), promediando sobre todos los posibles valores de los parámetros \(\theta_i\), según las distribuciones a priori.
💡 Interpretación: Nos dice qué tan bien explica el modelo los datos, considerando todas las incertidumbres en los parámetros.
¿Por qué es difícil calcular la verosimilitud marginal?
En modelos complejos (como los filogenéticos o de sustitución de secuencias), esa integral es imposible de resolver de forma exacta.
Tiene muchos parámetros y espacios de probabilidad muy grandes.
Por eso, necesitamos métodos numéricos que nos ayuden a estimarla.
Solución: Métodos basados en MCMC
➡️ Aquí es donde entran Stepping-Stone Sampling y Path Sampling, que son métodos basados en MCMC (Markov Chain Monte Carlo).
Ambos métodos:
Nos permiten estimar la verosimilitud marginal de manera aproximada pero con gran precisión.
Son más robustos y confiables que intentar calcular la integral directamente.
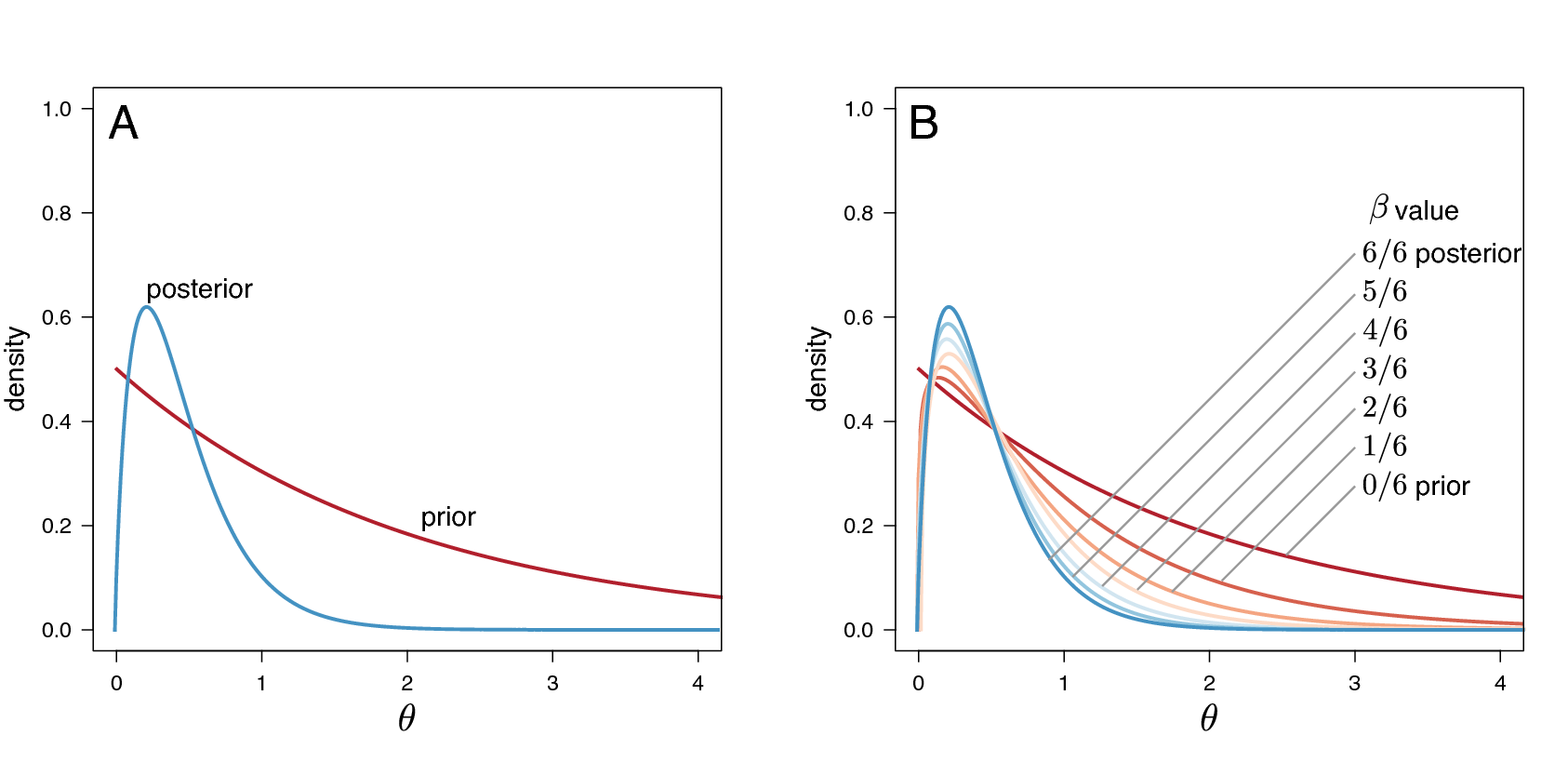
En la figura 6 piedras:
- 6 stones (piedras) significan 6 powers (β):
β = 0/6, 1/6, 2/6, 3/6, 4/6, 5/6, 6/6
O sea: 0, 0.166, 0.333, 0.5, 0.666, 0.833, 1.
Cada una te da una mezcla distinta de prior y posterior, y en cada una corres un MCMC.
β = 0/6 = 0 → solo prior.
β = 6/6 = 1 → solo posterior.
Intermedios (0 < β < 1) → mezcla de prior y posterior.
🌉 Stepping-Stone Sampling
🔹 ¿Qué hace?
Divide el camino entre la prior y la posterior en pequeños pasos (piedras).
En cada piedra, se hace una simulación MCMC para obtener información de ese punto.
Al final, suma toda la información para calcular la verosimilitud marginal.
🔹 Analogía:
Es como cruzar un río saltando por piedras, donde cada piedra es una mezcla distinta de prior y posterior.
🛤 Path Sampling
🔹 ¿Qué hace?
En vez de ir por piedras, hace un camino continuo desde la prior hasta la posterior.
Va midiendo la log-verosimilitud a cada paso.
Al final, suma (integra) toda esa información.
🔹 ¿Cómo se hace?
- Calcula el área bajo la curva de log-verosimilitud vs β.
🔹 Analogía:
Es como caminar por todo el río, sin saltos, y anotar cómo cambia la corriente a cada paso.
Stepping-Stone Sampling y Path Sampling en Revbayes
Este método calcula un vector de potencias (powers) a partir de una distribución beta, y luego realiza una simulación MCMC para cada valor de esa potencia, elevando la verosimilitud a esa potencia.
En esta implementación, el vector de potencias comienza en 1 (donde la verosimilitud se parece a la posterior), y va disminuyendo gradualmente hacia 0, acercándose a la prior.
Este procedimiento para estimar la verosimilitud marginal es válido para cualquier modelo en RevBayes. Primero, creamos una variable que contiene el análisis de power-posterior. Para eso, debemos indicar el modelo, los movimientos (moves), los monitores, y el nombre del archivo de salida. El argumento cats define el número de piedras (stepping stones).
Descarga el script para este ejercicio:
📥 Diversificacion de Eupomphini con tres intervalos
Comando para definir el análisis de power-posterior:
pow_p = powerPosterior(mymodel, moves, monitors, "output/model1.out", cats=50)- cats=50: número de piedras (50 pasos entre prior y posterior).
Importante: hacer “burn-in” antes de empezar:
Antes de empezar el análisis real, hacemos un burn-in para que la simulación no empiece desde un valor raro, sino desde un lugar donde ya la MCMC está estable.
pow_p.burnin(generations=10000, tuningInterval=1000)- Corre 10,000 generaciones antes de empezar a recolectar datos.
- Ajusta los movimientos cada 1000 generaciones.
Ahora, correr el análisis de power-posterior:
pow_p.run(generations=1000)- Corre 1,000 generaciones por cada piedra (por cada valor de β).
- Con 50 piedras (cats), harás 50 simulaciones MCMC distintas (una por cada β).
Cuando termina, hacer el cálculo de Stepping-Stone Sampling: Ya que se guardaron los resultados de cada piedra en el archivo, podemos crear un objeto para calcular la verosimilitud marginal por Stepping-Stone:
ss = steppingStoneSampler(file="output/model1.out", powerColumnName="power", likelihoodColumnName="likelihood")- powerColumnName: nombre de la columna con los β (normalmente “power”).
- likelihoodColumnName: nombre de la columna con las verosimilitudes (normalmente “likelihood”).
Para obtener la verosimilitud marginal por Stepping-Stone Sampling:
write("Stepping stone marginal likelihood:\t", ss.marginal() )Si quieres también Path Sampling (opcional y recomendable para comparar): Usa el mismo archivo para crear un estimador con path sampling:
ps = pathSampler(file="output/model1.out", powerColumnName="power", likelihoodColumnName="likelihood")Para calcular la verosimilitud marginal por Path Sampling:
write("Path-sampling marginal likelihood:\t", ps.marginal() )¿Cómo comparamos los modelos con Factores de Bayes?
🔑 Paso 1. Recordemos qué es el Factor de Bayes (BF):
El Factor de Bayes compara dos modelos, por ejemplo:
\(M_0\): Modelo simple (ej. Diversificación con 3 intervalos).
\(M_1\): Modelo complejo (ej. Diversificación con 5 intervalos).
🔑 Paso 2. ¿Cómo lo calculamos?
⚠️ Importante: Las verosimilitudes marginales se guardan como log-verosimilitudes (log-marginal likelihoods), porque son números muy pequeños problema de desbordamiento numérico.
Por eso, usamos la forma logarítmica del Factor de Bayes, que llamamos K:
\[ K = ln[BF(M_0, M_1)] = ln[P(X | M_0)] - ln[P(X | M_1)] \]
⚙️ Donde:
\(ln[P(X | M_0)]\): log-verosimilitud marginal del modelo simple (\(M_0\)).
\(ln[P(X | M_1)]\): log-verosimilitud marginal del modelo complejo (\(M_1\)).
Paso 3. Interpretar K:
| Valor de \(K\) | Interpretación | Modelo preferido |
|---|---|---|
| \(K > 1\) | Soporte a favor de M0 | M0 (modelo simple) |
| \(K < -1\) | Soporte a favor de M1 | M1 (modelo complejo) |
| \(-1 < K < 1\) | Sin preferencia clara entre los modelos | Ninguno claramente mejor |
Nota: Para convertirlo a Factor de Bayes “real”, solo elevas \(e^k\), pero normalmente usamos \(K\) directamente para comparar.
Ejemplo (con números inventados para ilustrar):
Tabla 1. Probabilidades marginales:
| Modelo | Path Sampling (lnL) | Stepping-Stone (lnL) |
|---|---|---|
| \(M_0\) - Diversificación con 3 intervalos | -120.5 | -119.8 |
| \(M_1\) - Diversificación con 5 intervalos | -122.1 | -122.0 |
| \(K\) | \((-120.5) - (-122.1) = 1.6\) | \((-119.8) - (-122.0) = 2.2\) |
Interpretación según la escala de Jeffreys:
| Valor de \(K\) | Interpretación |
|---|---|
| 0 a 1.16 | Mención mínima (débil). |
| 1.16 a 2.3 | Evidencia sustancial. |
| 2.3 a 4.6 | Evidencia fuerte. |
| > 4.6 | Evidencia decisiva. |
💡 En el ejemplo:
Con \(K\) = 2.2 (SS) → Evidencia sustancial a favor de \(M_0\).
Con \(K\) = 1.6 (PS) → También evidencia sustancial a favor de \(M_0\).